On the ionospheric conductivity

Three conductivities in the ionosphere
Equation of the conductivity in the ionosphere
Two dimensional conductivity

Ionospheric conductivity model (height profile)
Global ionospheric conductivity model

---

Introduction
The ionosphere is the region where plasma density is maximum in the Earth's upper atmosphere. Its altitude ranges almost from 60 to 1000 km. It acts not only as the reflection or absorption layer of the radio wave, but as an electric current layer. The ionospheric currents cause large part of the variation of the geomagnetic field, although most of the geomagnetic field itself is generated by the dynamo action in the Earth's core. The currents flow according to the Ohm's law, but the electric conductivity is anisotropic because of the effect of the geomagnetic field, and three conductivities are defined. Those are parallel, Pedersen and Hall conductivities, and additionally two dimensional conductivity is used for some purposes. Unit of these conductivities is S/m (=1/(Ωm)), and that of the height integrated conductivity is S. Their meanings are as follows:

Parallel conductivity Parallel conductivity is for the direction parallel to the magnetic field line and denoted as "σ0". This is same as that when there is no magnetic field, and much larger than Pedersen and Hall conductivities in the ionosphere. Terms of "longitudinal conductivity" and "direct conductivity" are also used. Pedersen conductivity Pedersen conductivity is for the direction vertical to the magnetic field and parallel to the electric field. It is denoted as "σ1". Hall conductivity Hall conductivity is for the direction vertical to both the magnetic and electric fields. It is denoted as "σ2". In the ionosphere this conductivity is due to the drift motion of the electron (ExB drift) and maximum in the E region where only electron practically drifts to the direction of ExB.

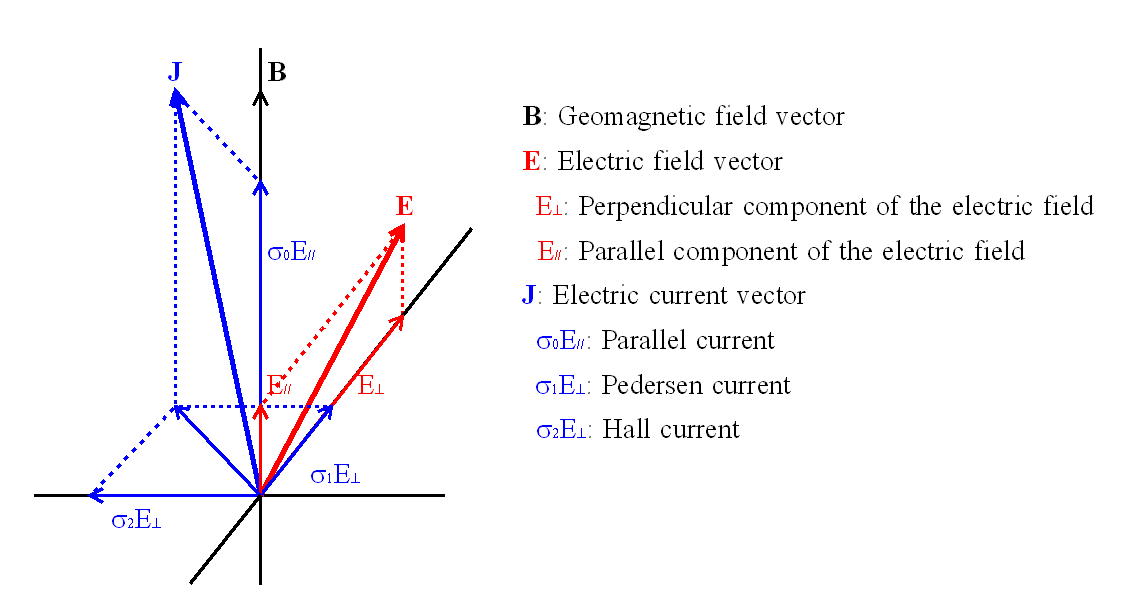Relationship between electric field and current in the ionosphere 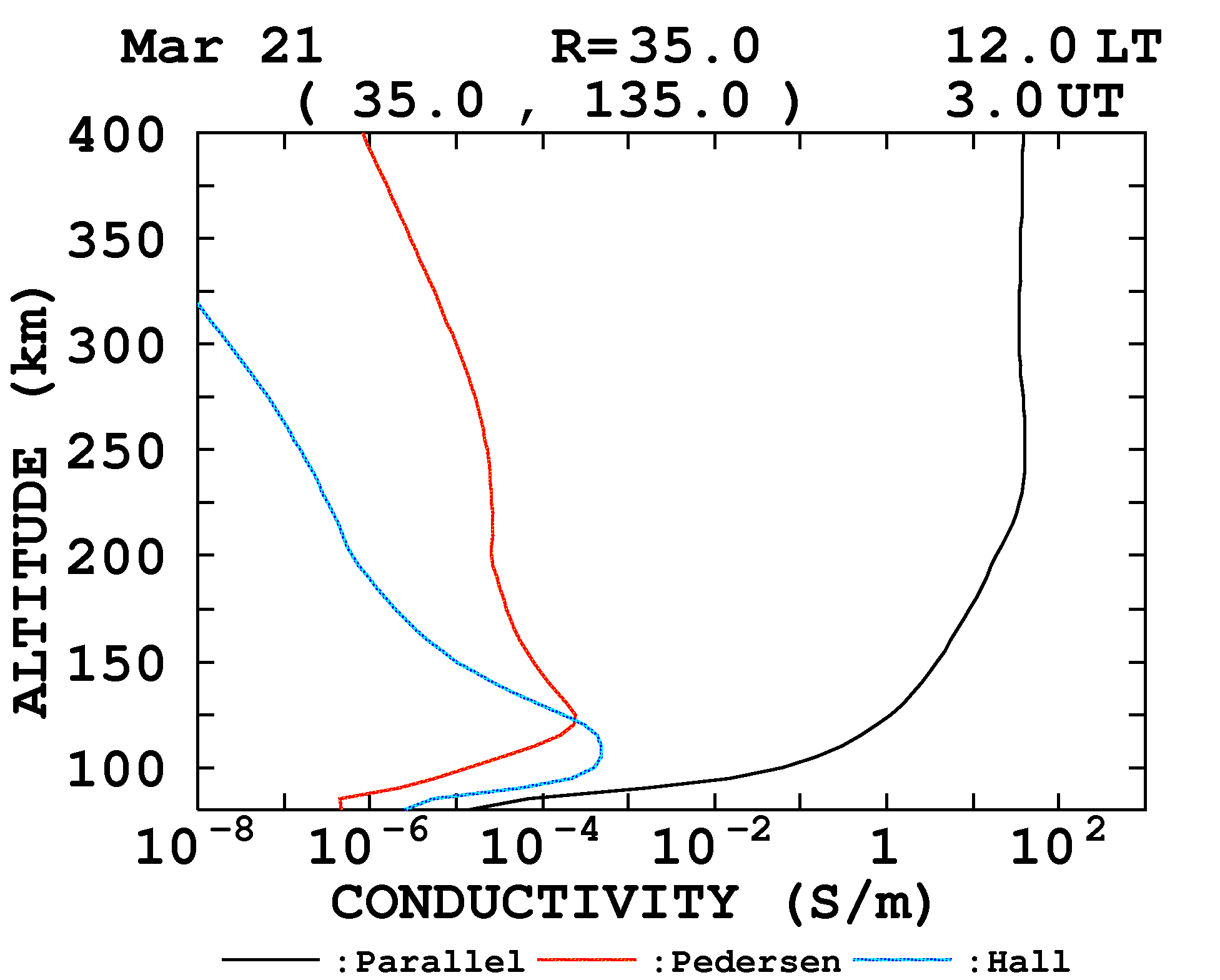An example of the daytime height profile of the ionospheric conductivity. An example of the daytime height profile of Black, red and blue lines represent Parallel, Pedersen and Hall conductivities, respectively. The conductivity depends on various parameters such as location, time, season and solar activity. For example, the conductivity at night reduces to one several-tenths of that at noon.

Equation of the ionospheric conductivity Equations for parallel, Pedersen and Hall conductivities in the ionosphere are given by Maeda (1977) as follows: σ0 = (ne*e2)/(me*νe) σ1 = σ0*((1 + κ)*νe2) /((1 + κ)2*νe2 + ωe2) σ2 = σ0*ωe*νe /((1 + κ)2*νe2 + ωe2) where κ = (ωe*ωi)/ (νe*νi),    νe = νen + νei,    νi = νin ne: electron density νen: electron-neutral collision frequency νei: electron-ion collision frequency νin: ion-neutral collision frequency ωe: electron cyclotron frequency ωi: ion cyclotron frequency e: a bare electric charge (1.602*10-19 C) me: electron mass (9.109*10-31 kg) Reference: Maeda, K., Conductivity and drift in the ionosphere, J. Atmos. Terr. Phys., Vol.39, 1041-1053, 1977. Two dimensional conductivity Word of "Layer conductivity" is also used. The ionosphere can be regarded as a thin layer in some cases because scale length of vertical direction is smaller than that of the horizontal direction. Under such treatment two dimensional conductivity is defined as follows: When we take the coordinate in which X is magnetic north and Y is magnetic east, and horizontal electric field is (EX, EY), current density (jX, jY) is expressed as: jX = σXXEX + σXYEY jY = - σXYEX + σYYEY where σXX, σYY and σXY are the elements of the two dimensional conductivity. They can be written using σ0, σ1 and σ2 and geomagnetic dip angle I   as follows: σXX = (σ0*σ1)/(σ1*cos2I + σ0*sin2I) σYY = (σ0*σ1*sin2I + (σ12 + σ22)*cos2I)/(σ1*cos2I + σ0*sin2I) σXY = (σ0*σ2*sinI)/(σ1*cos2I + σ0*sin2I) In most cases height integrated values (frequently denoted as ΣXX, ΣYY and ΣXY) of σXX, σYY and σXY are used because of the assumption in the derivation.