 電離層電気伝導度の式
電離層電気伝導度の式
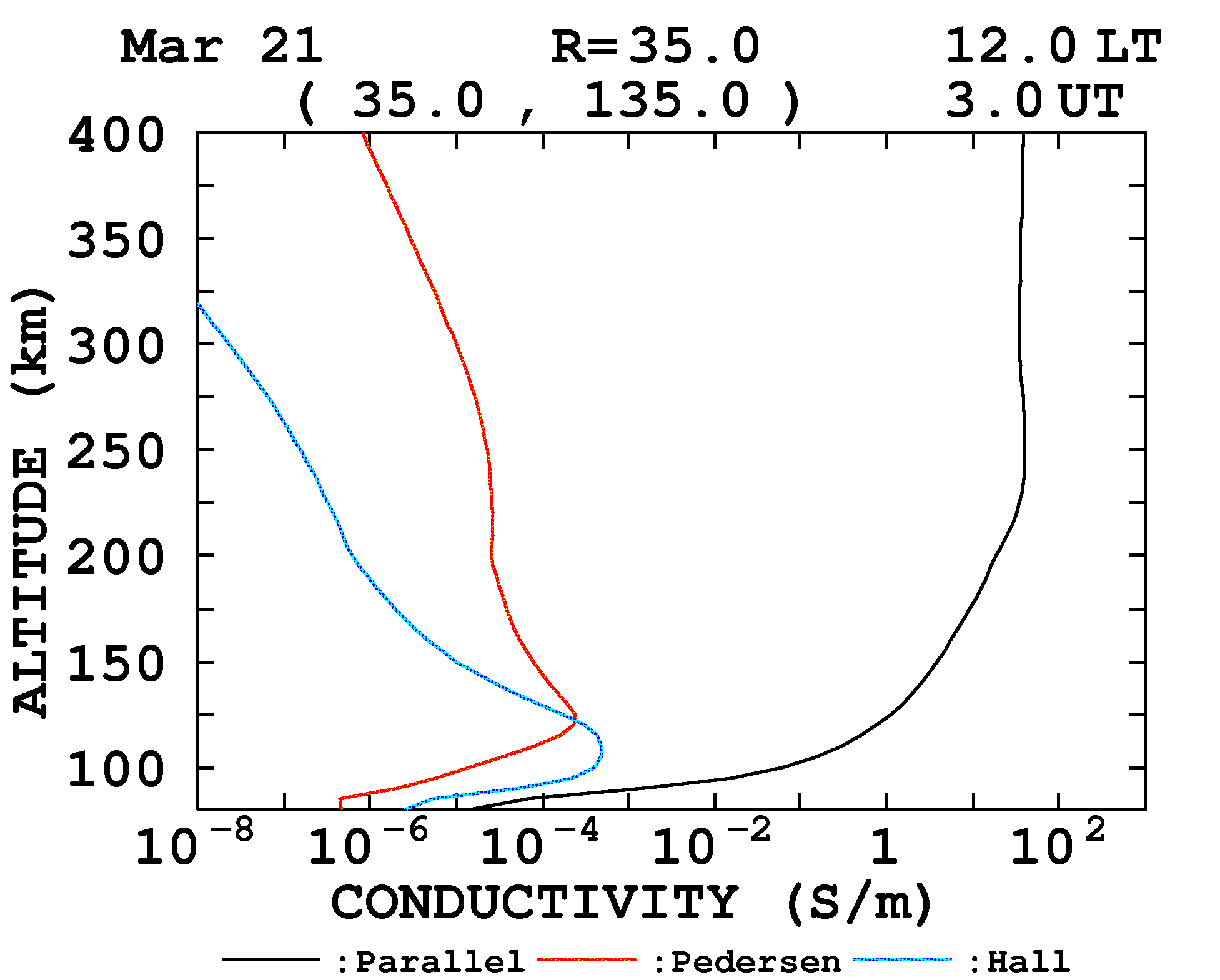
- 電離層での上記3伝導度はMaeda (1977)
により3流体近似に基づき以下の式で表される:
σ0 =
(ne*e2)/(me*νe)
σ1 =
σ0*((1 + κ)*νe2)
/((1 + κ)2*νe2 +
ωe2)
σ2 =
σ0*ωe*νe
/((1 + κ)2*νe2 +
ωe2)
ここで、
κ = (ωe*ωi)/
(νe*νi),
νe = νen + νei,
νi = νin
ne: 電子密度
νen: 電子-中性粒子の衝突周波数
νei: 電子-イオンの衝突周波数
νin: イオン-中性粒子の衝突周波数
ωe: 電子の旋回角周波数
ωi: イオンの旋回角周波数
e: 素電荷 (1.602*10-19 C)
me: 電子の質量 (9.109*10-31 kg)
文献:
Maeda, K., Conductivity and drift in the ionosphere,
J. Atmos. Terr. Phys., Vol.39, 1041-1053, 1977.
 2次元伝導度
(Two dimensional conductivity)
電離層は一般に鉛直方向のスケールが水平方向のそれと比べて小さいので、
鉛直方向には無限に薄い薄層として扱われることがあり、
そのような扱いをしたときの伝導度を2次元伝導度という。
層伝導度 (Layer conductivity) ということもある。
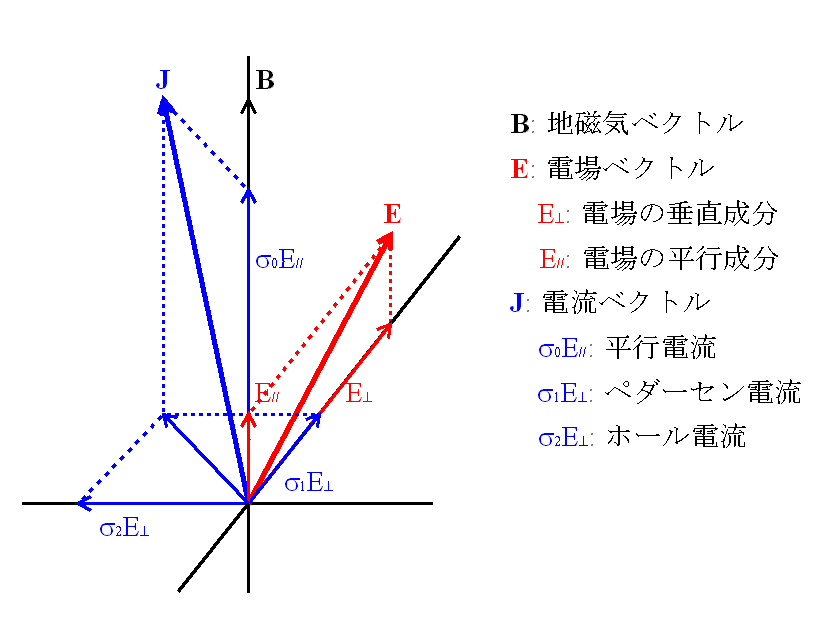
具体的には、磁北をX、磁東をYとした座標系で、
水平面内の電場と電流密度ベクトルをそれぞれ
(EX,EY)、(jX,jY)として、 2次元伝導度
(Two dimensional conductivity)
電離層は一般に鉛直方向のスケールが水平方向のそれと比べて小さいので、
鉛直方向には無限に薄い薄層として扱われることがあり、
そのような扱いをしたときの伝導度を2次元伝導度という。
層伝導度 (Layer conductivity) ということもある。
具体的には、磁北をX、磁東をYとした座標系で、
水平面内の電場と電流密度ベクトルをそれぞれ
(EX,EY)、(jX,jY)として、
jX =
σXXEX + σXYEY
jY =
-σXYEX + σYYEY
と表現したときのσXX,σYY,σXYであり、
上記3伝導度σ0, σ1, σ2と地磁気伏角 Iを用いて、
σXX =
(σ0*σ1)/(σ1*cos2I +
σ0*sin2I)
σYY =
(σ0*σ1*sin2I +
(σ12 +
σ22)*cos2I
)/(σ1*cos2I +
σ0*sin2I)
σXY =
(σ0*σ2*sinI)/(σ1*cos2I +
σ0*sin2I)
とあらわされるが、その性質上高さ方向について積分された値
(それぞれΣXX, ΣYY,
ΣXYと略記される)
がより多く用いられる。
|



 2次元伝導度
(Two dimensional conductivity)
2次元伝導度
(Two dimensional conductivity)